罗伯特·马修斯(Robert Matthews)的基础概率问题
http://web.wenxuecity.com/BBSView.php?SubID=kxtw&MsgID=7768
假定一项疾病检验的准确率为95%,即患病者的检验结果呈阳性的概率,和未患病者的检验结果呈阴性的概率都是95%。已知被测人群中这种疾病的患病率为千分之一.那么,已知一个人的检验结果呈阳性,则他确实患病的可能性有多大?半数受试人完全没有意识到基础概率的影响,他们的答案是95%. 只有不到五分之一的人给出了正确答案:此人患病的概率不足2%.。’
这个例子猛一看似乎很有道理,但总觉得广泛使用的辅助检查,大部分的都有假阳性和假阴性的问题,如果阳性结果对诊断疾病如此没有帮助(可能性不足2%),全世界的医院岂不是都在开玩笑?这样的玩笑可真是国际玩笑了。
问题究竟出在哪里?罗伯特的概率计算没有问题。按照他的计算方法,应该这么理解:随机选取一个人,他的患病概率是 千分之一,即:0.1%. 而呈现阳性的人群中患病的概率是2%,换句话说,呈现阳性的被检查者,患病的可能性是 普通人群的20倍。从这个意义上来看,并不像作者所说的那么悲观。
作者还混淆了一个概念,阳性率95%指的是:本来应该阳性的5%没有呈现阳性,即有5%的假阴性。假如检查阳性就可以诊断某种疾病,将有5%的漏诊。而正常人群中,假阳性率为5%,也就是说被检验者中将有5%的可能性被误诊。因此,对病人来讲,如果检查是阳性的一定是患病。检查阳性的病例中有多大可能患病哪?那就是,100%-减去假阳性的可能性5%,即100%-5%=95%。(这里和漏诊没有关系)我认为,马氏错误地使用的基础概率的整体。临床检验不是人群的普查。临床检验时有高度针对性的,也就是说:医院检查的这个人群已经不是普通人群,这个人群的患病率一定大大高于普通人群!
考虑的对否,请概率知识丰富的同学指正。
附录:
你的预测有多准?
作者:罗伯特·马修斯(Robert Matthews)
翻译:yimin
原文:
http://www.newscientist.com/article/mg15320724.000-how-right-can-you-be.html
译文首发在译言网上:http://www.yeeyan.com/articles/view/yimin/9204
你准备去集市上买点东西,大概需要一个小时左右就可以回来。不过天气预
报说有雨,你该怎么办?假如你知道,预报的准确率在80%左右。那么,你需要
一把雨伞的可能性是80%,不是吗?非也,下雨的可能性其实只有30%.
这个结论看起来有些奇怪,不过这与预报员的夸大其词或天意弄人可没什么
关系。人们在理解概率问题时,有一种奇特的数学效应总会使我们出错,刚才提
到的只是其中一个例子。这种效应影响极为广泛,不仅阴晴雨雪这类日常预测受
其影响,从地震的预测到谋杀案的目击证词,没一个逃得出它的掌心。
隐藏在幕后的那股力量就是"基础概率效应"。简单地说,我们经常需要预测
某件事在将来是否发生,而这种预测的效果会受到基础概率的影响。所谓基础概
率,就是指我们从经验数据中得到的某件事的实际发生概率。当你预测任何罕发
事件时,这种影响就会非常明显。即使你认为自己的预测是非常准确的,你的准
确预测也会淹没在大量错误预测之中。
降雨的预报是个经典的例子。英国气象局对于降雨的预报准确率为80%左右,
这很容易让人产生这样的预期:如果气象局预报有雨,那么八成就真的要下雨。
这种推测之所以是错的,是因为它忽视了降雨的基础概率。
仔细一想就会发现这一点有多重要。即使是最蠢的预报员也能以惊人的准确
率预报智利阿塔卡马沙漠的降雨:在那里,数十年才下一场雨。因此,如果想以
近乎100%的准确率预报那里的天气,你只需说:"各位观众,明天不会下雨。"
对英国变化无常的天气来说,情况就要复杂一些,但基础概率对天气预报的
可靠性仍然有巨大的影响。英国的小时降雨基础概率是0.1,就是说,在任何一
个小时内,降雨的可能性均为十分之一。这个基础概率决定了我们应该对80%准
确率的降雨预报抱有几分信任。
为什么这么说呢?假设你一年内会进行100次这样的"一小时购物"。10%的小
时降雨基础概率意味着你的90次购物之旅不会碰上下雨,另外10次则没那么幸运。
在这10次下雨天气中,天气预报将会准确预报其中的8次,因为它的准确率为80%.
不过80%的准确率同时也意味着20%的不准确率——因此气象局将会把18次晴
好天气预报成有雨(译者注:18=90*20%)。加起来,共有26次预报有雨,其中8
次是准确的。所以,尽管预报的准确率高达80%,但在预报有雨的日子里,出门
的一个小时内真碰上雨的可能性只有30%.
被放大的误差
实际上,大量晴好天气将降雨预报中的微小误差放大了,以致准确的预报被
淹没在错误预报之中。(参看本文"计算罕发事件的发生概率")这清楚地提醒我
们是否该认真对待天气预报。在最近的一期《自然》(Nature)杂志上,我证明
了:如果你只需出门一两个小时,而且可以忍受偶尔被淋湿,那么,即使气象局
预报说有暴雨,最佳的做法仍是:不带伞。
除了帮助我们决定是否带伞,基础概率效应也解释了为何当今准确率颇高的
天气预报仍然饱受质疑。在最新一期的《当代数学》(Mathematics Today)中,
我认为这是因为人们出门的次数和呆在户外的时间不够长,等不到下雨的那一刻。
如果你打算在户外待上一整天,那么你可得认真看天气预报:日降雨的基础概率
是0.4,这就使得在预报有雨的日子里,下雨的概率比不下雨的概率高出近两倍
(译者注:给定预报的准确率为80%,此时当天下雨的概率是73%,是不下雨的概
率27%的近三倍)。可以这么说,一件事越常见,就越容易准确地预测。
这么一说,基础概率效应似乎是显而易见的。可让心理学家们不解的是:既
然如此,为何我们在碰到类似问题时总是出错?斯坦福大学已故的阿莫斯·特沃
斯基(Amos Tversky)和普林斯顿大学的丹尼尔·卡纳曼(Daniel Kahneman)
开创性地研究了人类对于不确定性信息的认知能力。他们的研究成果长期以来被
广泛引用,证明人类在处理概率问题时会变得无可救药,尤其在处理与基础概率
有关的问题时。经常被引用的一个例子就是所谓的"出租车问题"(Cab
Problem)。
蓝车还是绿车?
一个城镇中发生一起出租车夜间肇事逃逸案,这个城镇只有两家出租车公司
营运:一家的车子是绿色的,数量占所有出租车总数的85%,另一家的车是蓝色
的,占15%。一个目击者声称肇事车是蓝车。警察在出事当夜相同的环境下测试
得到目击者的判断准确率为80%. 那么,肇事车确实是蓝车的可能性有多大?
如果对基础概率一无所知,很可能回答:80%——这是人们直觉倾向的答案。
但正确的答案却是41%(用列联表可以很容易得到这个结果)(译者注:列联表
的使用见本文最后一部分)。占多数的绿色出租车意味着:被目击者错认为蓝车
的绿车数量会大于他认对的蓝车数。结论是:警察抛硬币来决定肇事者更靠谱。
有人会把这样的问题仅仅当作智力游戏,但医生在做出生死攸关的决定时,
也会受到基础概率的影响。哈佛大学医学院发表于1978年的一项研究中,60名受
试的教师和学生被问到以下问题:假定一项疾病检验的准确率为95%,即患病者
的检验结果呈阳性的概率,和未患病者的检验结果呈阴性的概率都是95%。已知
被测人群中这种疾病的患病率为千分之一. 那么,已知一个人的检验结果呈阳性,
则他确实患病的可能性有多大?
半数受试人完全没有意识到基础概率的影响,他们的答案是95%. 只有不到
五分之一的人给出了正确答案:此人患病的概率不足2%.
令人担心的是,对于医务工作者的其它类似研究都得出同一结论:受试者普
遍头脑混乱。在诊断阶段如果忽略基础概率的影响,将会造成大量的过度医疗。
不过,一些心理学家开始问:"如果这种研究以更加浅显的形式进行呢?"最近发
表在《行为科学和脑科学》(Behavioral and Brain Sciences)上的一篇基础
概率综述文章中,德克萨斯大学奥斯汀分校的乔纳森·科勒(Jonathan Koehler)
指出,许多研究都预先设定受试者无法正确回答问题,这些研究与其说揭示了我
们认知概率信息的能力,还不如说暴露出他们提问的方式有问题。
他认为类似"出租车问题"的那些难题总是语焉不详。比如,你可以说:重要
的基础概率不是蓝车在车辆总数中所占的比例,而应该是蓝车在有夜间事故记录
的车辆中所占的比例。毕竟,蓝车虽少,但也许他们的安全记录普遍更差呢?这
个基础概率并没有给出,受试者只能瞎猜。科勒说,如果你没有给出受试者认为
重要的信息,那么他们犯错误就没什么好奇怪的。
以正确的方式提问
科勒补充道,最近研究显示,如果以频率的形式而非概率的术语提问,受试
者对基础概率的认知会好许多。比如,不要求他们估计检验呈阳性的人确实患病
的概率,而是要求他们估计100个检验呈阳性的人当中,有几个确实患了病。
这种措辞的微妙变化带来了全新的结果,至少看起来是这样。在加州大学圣
巴巴拉分校的勒达·考斯米德和约翰·托比(Leda Cosmides and John Tooby)
去年发表的研究中,受试学生回答了与哈佛大学研究中类似的疾病诊断问题。当
问题以概率的术语提出来时,他们表现同样糟糕;可当问题以频率的形式提出来
时,许多学生都意识到了基础概率的影响。
这个发现对于如何训练医生解读检验结果有着清晰且重要的意义。俗话说"
罕见的病不容易诊断",话是没错,可这对诊断没什么帮助,何况陪审团也不会
认可对医疗事故的这种解释。
陪审团和法官经常碰到包含概率信息的证据。更好地理解基础概率效应会对
他们的工作颇有助益。有关DNA鉴定的证据特别容易受到基础概率的影响。许多
法学专家对这种证据在法庭上的出示表示担忧,因为陪审团、法官和法医专家很
可能误解DNA匹配概率的真实含义。(参见《增加公正的机率?》,《新科学家》
杂志,1994年6月15日,12-13页)"Improving the odds on justice?", New
Scientist)
即使证据显得无可置疑,忽略基础概率也会导致误判。如果对被告不利的证
据非常少——即其犯罪的基础概率很低——那么就算DNA匹配程度极高,我们仍
有权利对"被告就是罪犯"的论断表示合理的怀疑。
回到现实中来
忍辱负重的气象局如果更加重视基础概率,他们也能从中获益。考虑到天气
预报的难度,气象局已经做得相当不错了。如果他们能在预报时考虑基础概率,
比如在预报时说:"如果您只出门一小会儿,那么很可能不用带伞。"这样他们可
能会得到更多的认可。
理解基础概率效应能帮我们更好地预测天气,处理法庭上的证据,以及诊断
疾病,不仅如此,它给我们的核心启示——罕发事件很难预测——还能帮我们节
省一大笔很可能有去无回的科研经费。
以地震预测为例。过去100年里,地震学家将大笔的经费投入到地震预测研
究中,收获廖廖。尽管如此,研究者们仍固执地寻找那些可能帮我们预测大地震
的种种"前兆"。
基础概率效应清楚地告诉我们,这种执着误入了歧途。预测像神户地震这种
强度的大地震当然很了不起,可这样的地震极其罕见,大约50到100年发生一次。
这么低的基础概率意味着,如果要让决策者下定决心,命令大规模人口转移的话,
任何地震前兆都必须极其可靠。
粗略的计算显示,任何有价值的地震预测手段,其观测的地震前兆的准确率
必须达到98%以上。到目前为止,任何所谓的地震前兆都远未达到这个准确率。
而且,不断有证据表明,地震就像雪崩一样,本质上是极不稳定的"临界"现象
(译者注:关于临界现象,可以参看
http://www.-reader.org/blogs/fangzhouzi/2008/06/05/%E5%83%8F%E6%B2%
99%E5%A0%86%E4%B8%80%E6%A0%B7%E5%B4%A9%E5%A1%8C/)。所以,找到高度准确
的地震前兆的可能性微乎其微。
虽然长期以来基础概率效应主要出现在心理学研究当中,但它远非仅供学者
娱乐消遣的简单逻辑游戏。理解它可以帮助我们更好地做出决策,并避免无用功。
* * *
计算罕发事件的发生概率
如果有预报说某件事会发生,则可以用概率论来计算其发生概率,可这办法
不仅枯燥而且不易理解。"列联表"是个更便捷、易懂的工具。最简单的列联表中,
两列代表两种可能的实际状态,比如下雨和没下雨;两行代表相应的预测,比如
预报有雨和预报无雨,只要几次简单的算术运算,你可以填满这个表格,并从中
得到任何你感兴趣的事件概率。
以降雨预报为例。有两项关键数据:每小时的降雨基础概率10%,以及预报
准确率80%. 这意味着在100次为期一小时的外出中,有10次会碰上下雨,90次无
雨。把这写到每列的标题中去。
先来填第一列,标题为"下雨",我们知道,在确实下雨的情况下,给定预报
的准确率为80%,则预报有雨的次数为8次(10*0.8),预报无雨的次数为2次
(10*0.2),依次填入第一列。
同样地,在90次无雨的外出中,预报有80%是准确的,即预报无雨72次
(90*0.8),预报有雨18次(90*0.2),填入相应单元格内。这样表格就完整了,
所有信息一目了然。
比如,从第一行中,我们马上可以知道在这100次外出中,共有26次预报有
雨,可实际上只有8次是准确预报的,准确率仅为30%. 不过,在74次无雨预报中,
有72次是准确的预报,准确率高达97%. 所有的预测系统,从地震预测到癌症诊
断,只要给定事件基础概率和预测准确率,都可以用这种方法分析相关的概率。
下雨(10) 没下雨(90)
预报 有雨 8=10*80% 18=90*20%
预报 无雨 2=10*20% 72=90*80%
预报有雨次数 8+18=26
准确预报次数 8
准确率 8/26=30.8%
回复 1:我觉得罗伯特·马修斯错误应用了条件概率概念. 0.1%的患病率,与95%的准确率,不是相关事件.
有病的人如果检查是95%阳性,5%阴性。假定是“有病”。
没病的人如果检查是95%阴性,5%阳性。假定是“无病”。
都是条件概率。
另外,你也可以看出来,95%的准确率是很好的检验手段了。但,如果只有2%地把握判断有没有病,几乎等于没说。要是这样的话,上医院还不如烧香。 ^_^
回复 2:
假设1000万人,1万人患病。
检验准确率95%。一万病人中有9500阳性,500阴性。999万没患病的人中,9490500人阴性,499500人阳性。
检验阳性人数:509000人,其中患病人数:9500人,站检验阳性人数的1.8664%。
患病 (10000) 没病 (9990000)
检验 阳性 (10000*95%=9500) (9990000*5%=499500)
检验 阴性 (10000*5%=500) (9990000*95%=9490500)
检验阳性人数 499500+9500=509000
检验准确人数 95000
准确率 95000/509000=18.664%
问题的关键是:临床检验不同于普查,在诸多检验中,进行千万人普查的机会是不多的。举个例子:甲胎球蛋白阳性来诊断肝癌,在10000万人中,永远不可能所有5%的假阳性全被查出来。换个说法:临床检查一共查出100例阳性样品,问其中的假阳性占多少?我觉得答案应该是5%。临床检查并不是人群的随机抽样,因此整体人群的患病率在这里不起作用,换句话:临床检查的人群总体不等于正常人群总体。医生只会给肝区疼痛,有慢性肝炎和肝功不正常等怀疑可能患肝癌的人开甲胎球蛋白的专门检查。
Subscribe to:
Post Comments (Atom)
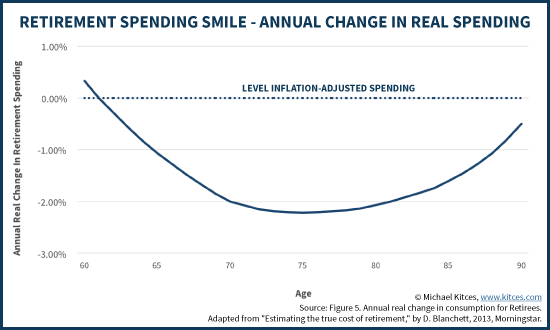
如何发掘出更多退休的钱?
如何发掘出更多退休的钱? http://bbs.wenxuecity.com/bbs/tzlc/1328415.html 按照常规的说法,退休的收入必须得有退休前的80%,或者是4% withdrawal rule,而且每年还得要加2-3%对付通胀,这是一个很大...
-
魏杰教授这篇演讲,深入浅出,把未来几年的经济形势讲的非常透彻。 魏杰:我和大家一起对未来一段时间做一个交流,可能在座的知道从2018年3月份开始,中国社会生活出现了六个很严重的现象。 第一个现象 ,大量的中小企业反映企业非常难做,压力很大。既有成本压力,也有资金...
-
如何发掘出更多退休的钱? http://bbs.wenxuecity.com/bbs/tzlc/1328415.html 按照常规的说法,退休的收入必须得有退休前的80%,或者是4% withdrawal rule,而且每年还得要加2-3%对付通胀,这是一个很大...
-
以下内容摘编自中文版《如何让孩子成年又成人》。 1. 另辟蹊径 我们都希望孩子在离家的时候,可以产生 “我觉得我可以,我觉得我行” 的心态。 这种心态的另一种表述是 “自我效能” 。它意味着相信自己有能力完成任务、实现目标及把把控局面。它意味着你相信自己做事情的能...
No comments:
Post a Comment