有一个圆形的湖,直径100米。一只老鼠在湖心处游泳,岸边来了一只猫。
猫很饿啊,到嘴边的美味自然不会放过,可是猫不会游泳,只好绕着湖岸追老鼠跑。猫的速度是10m/s,那么,老鼠游泳速度至少要多少才能安全逃上岸呢?
解法一:
设老鼠的游泳速度为x(m/s);老鼠从圆心处开始沿着背向猫的一条半径往岸边游。老鼠需要游过的路程是50米,所花的时间是50/x;猫需要跑过的路程是50π米,所花的时间是50π/10;列不等式:
50/x<50π/10 ,
解不等式,得:x>10/π=3.18(m/s)。
老鼠游泳速度至少要快于3.18(m/s),才能安全逃上岸。
这肯定不是最好的答案。老鼠的游泳速度还可以比3.18(m/s)更小。
贴子相关图片:
解法二:
老鼠从圆心开始,先游到适当的半径r处,以半径r绕着圆心做圆周运动,使老鼠绕小圆一周所花的时间等于猫绕大圆(水池岸上)一周所花的时间,这样就可以保证在某个时刻和猫的距离为50+r(当然,不一定要做整个圆周运动,只要绕着圆心就行)。列方程:
rπ/x=50π/10 .
然后,老鼠从C点径直往岸边的A点游,力争先于猫到达A点.列不等式:
(50-r)/x<50π/10
联立二式解得:x<10/(π+1)≈2.4145(m/s)
还有比这更小速度的方案.
附图:
贴子相关图片:
解法三:
老鼠从圆心开始,先游到适当的半径r处,以半径r绕着圆心做圆周运动,使老鼠绕小圆一周所花的时间等于猫绕大圆(水池岸上)一周所花的时间,这样就可以保证在某个时刻和猫的距离为50+r.列方程:
rπ/x=50π/10 .
然后,老鼠从C点不再是径直往岸边的A点游,而是沿小圆的切线往岸边的D点游(当然要看猫跑的方向),力争先于猫到达D点。可知CD线段长为:√(R^2-r^2);CD弧长为:arccos((√R^2-r^2)/R)。列不等式:
(50^2-r^2)/x<50(π+arccos(√(50^2-r^2)/50)/10.
联立二式即可解得x的值。但是我不会解,因为它包含有反三角函数。有人用数值解法解出,老鼠的速度为x>2.1723m/s。
不用担心猫会转方向,因为猫和老鼠之间的距离在缩短,猫改变方向只会更有利于老鼠。
可以肯定,这个答案还不是最优的。
我在8楼的不等到号写反了,谢谢9楼朋友的指正!
贴子相关图片:
解法三:
老鼠从圆心开始,先游到适当的半径r处,以半径r绕着圆心做圆周运动,使老鼠绕小圆一周所花的时间等于猫绕大圆(水池岸上)一周所花的时间,这样就可以保证在某个时刻和猫的距离为50+r.列方程:
rπ/x=50π/10 .
然后,老鼠从C点不再是径直往岸边的A点游,而是沿小圆的切线往岸边的D点游(当然要看猫跑的方向),力争先于猫到达D点。可知CD线段长为:√(R^2-r^2);CD弧长为:arccos(√(R^2-r^2)/R)。列不等式:
√(50^2-r^2)/x<50(π+arccos(√(50^2-r^2)/50)/10.
联立二式即可解得x的值。但是我不会解,因为它包含有反三角函数。有人用数值解法解出,老鼠的速度为x>2.1723m/s。
回答24楼:
你说:“猫可以反向跑”。但是,别忘了:老鼠也可以反向游。只不过老鼠不是原路返回,而是转过一个方向,继续往岸边游。
请看解法二和解法三的前半部分:老鼠从圆心开始,先游到适当的半径r处,以半径r绕着圆心做圆周运动,使老鼠绕小圆一周所花的时间等于猫绕大 圆(水池岸上)一周所花的时间,即rπ/x=50π/10。此时,猫和老鼠的角速度相等。也就是说,在相同的时间内,猫和老鼠围绕圆心转过的角度相等,两 者相对所夹的圆心角始终为180度保持不变。此时,若猫反向跑,老鼠也可以反向游,两者相对所夹的圆心角始终为180度保持不变。这时,老鼠离岸边的距离 为50-r。
如果老鼠在某一时候,不再作圆周运动,而是沿小圆的切线方向从C点往D点游,此时,因为老鼠的旋转半径增大,而且运动方向与圆周产生一定夹 角,因此,老鼠此时的角速度小于猫的角速度,猫和老鼠之间所夹的圆心角(猫追赶老鼠方向的圆心角,即图左边BA弧)在减小,也就是说,猫和老鼠之间的距离 在缩短。
如图:当老鼠沿切线CD方向游到某一点F时(注意:这个F点哪怕是游出C点一点点),老鼠游过的圆心角为∠COF(即∠COI),而猫此时 的角速度大于老鼠的角速度,那么猫跑过的圆心角∠BOG就会大于∠COI。此时,猫和老鼠之间的圆心角∠GOI就小于180度。所以说,“不用担心猫会转 方向,因为猫和老鼠之间的距离在缩短,猫改变方向只会更有利于老鼠。”
如果猫硬要一意孤行,掉转方向往回跑。那么,当猫跑到与F点相对于圆心的H点时,老鼠也可以改变方向(但不是原路返回),以OI为对称轴,沿FD的对称线FI往岸边游。
不知我说清楚了没有?
贴子相关图片:
逃脱方案:
老鼠先向右走dx,顺带一个比dx还小得多的dy.
1.若猫向右走k倍的dx
则老鼠向左走dx,顺带一个比dx还小得多的dy.
(1)若猫继续向右走k倍的dx
则老鼠向左走dx,顺带一个比dx还小得多的dy.
①若猫不打算回头了,一直向右走
则老鼠一直向左走
结果:老鼠沿切线逃走,猫沿劣弧追.
②若猫回头向左走k倍的dx
则老鼠也回头向右走dx,顺带一个比dx还小得多的dy.
结果:经过这么一左一右一折腾,猫相当于静止不动,老鼠白赚了两个dy.
(2)若猫回头向左走k倍的dx
则老鼠也回头向右走dx,顺带一个比dx还小得多的dy.
结果:经过这么一左一右一折腾,猫相当于静止不动,老鼠白赚了两个dy.
(分析到这里,Fans忍不住骂一句:傻猫你就尽管换方向吧,老鼠凭着微不足道的dy不知不觉就逃脱了.)
2.若猫向左走k倍的dx
情况类似,不再敷述.
贴子相关图片:
回答: 证明在这里(revised) 由 竞选 于 2008-10-19 18:00:14
定义S1为:如果老鼠的速度小于或等于S1,则老鼠会被猫抓住,而当老鼠的速度大于S1时,老鼠可安全逃离此圆湖。这样定义的S1是存在的。
现在来证明:不存在这样一个老鼠的最小的速度S2使得老鼠能安全逃离此湖。
用反证法:假设这样的S2存在,则S2 > S1。定义S3=(S1+S2)/2,则从S3>S1及S1的定义知老鼠的速度为S3时老鼠可以安全逃脱。
又从S3
简而言之,就是:大于S1的最小实数是不存在的。
Friday, October 24, 2008
Subscribe to:
Post Comments (Atom)
如何发掘出更多退休的钱?
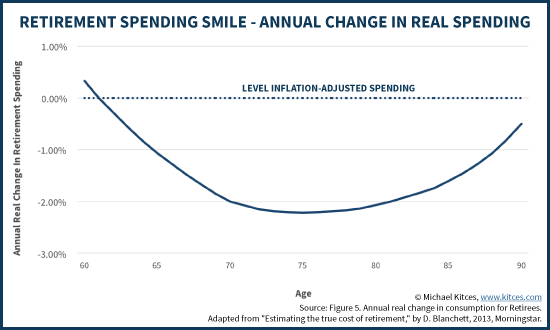
如何发掘出更多退休的钱? http://bbs.wenxuecity.com/bbs/tzlc/1328415.html 按照常规的说法,退休的收入必须得有退休前的80%,或者是4% withdrawal rule,而且每年还得要加2-3%对付通胀,这是一个很大...
-
魏杰教授这篇演讲,深入浅出,把未来几年的经济形势讲的非常透彻。 魏杰:我和大家一起对未来一段时间做一个交流,可能在座的知道从2018年3月份开始,中国社会生活出现了六个很严重的现象。 第一个现象 ,大量的中小企业反映企业非常难做,压力很大。既有成本压力,也有资金...
-
如何发掘出更多退休的钱? http://bbs.wenxuecity.com/bbs/tzlc/1328415.html 按照常规的说法,退休的收入必须得有退休前的80%,或者是4% withdrawal rule,而且每年还得要加2-3%对付通胀,这是一个很大...
-
以下内容摘编自中文版《如何让孩子成年又成人》。 1. 另辟蹊径 我们都希望孩子在离家的时候,可以产生 “我觉得我可以,我觉得我行” 的心态。 这种心态的另一种表述是 “自我效能” 。它意味着相信自己有能力完成任务、实现目标及把把控局面。它意味着你相信自己做事情的能...
No comments:
Post a Comment